Curious Corner

“Infinity is not a number, it’s an idea. An idea that transcends the boundaries of human understanding.”

— Anonymous

Infinity, in the realm of mathematics, is more than just an abstract concept – it is an enigma that has puzzled and fascinated mathematicians for more than a few millennia. While the origins of infinity stretch back to ancient Indian and Greek philosophy, it wasn’t until the 17th century that the notion of infinity took its modern shape. John Wallis, in 1655, introduced the infinity symbol (∞) to handle infinite series, while Isaac Newton used infinity to develop calculus. Yet, to this day and age infinity remains as elusive as ever.

Georg Cantor, the founder of set theory and the person who completely revolutionized the way mathematics interprets infinity, once remarked, ‘The essence of mathematics lies in its freedom‘. For him, infinity wasn’t a limitation – it was an opportunity to explore the endless depths of mathematics.

What is Infinity?

Fundamentally, infinity refers to something that has no bounds or limits. Unlike any number we can think of, infinity stretches beyond, it is very well visually represented by a never ending number line that keeps going on and on. Another reason why it is very hard to grasp is its abstract nature which seems so distant from our day to day life experience. Yet even in daily life we sometimes use the idea of infinity to describe something, be it our friends’ stupidity or the edge of the horizon.

Types of Infinity

While it may seem fairly logical to assume that the idea of infinity is singular, mathematicians have shown that some infinities are actually larger than others. Georg Cantor demonstrated this in the late 19th century with modern set theory.

Countable vs. Uncountable Infinity: The set of natural numbers (1, 2, 3, …) is an example of a “countable infinity“. Yet, the set of real numbers between 0 and 1 is an “uncountable infinity“—it’s larger than the infinity of natural numbers. Cantor’s Diagonal Argument is a famous proof that shows the distinction between these infinities.

Infinitesimals: While infinity represents boundlessness, infinitesimals are quantities that are infinitely small. They are central to calculus, where they help calculate things like rates of change (derivatives) and the areas under curves (integrals).

“IN THE MIND’S EYE, a fractal is a way of seeing infinity.”

― James Gleick, Chaos: Making a New Science

Infinity in Mathematics

Cantor’s Diagonal Argument: Cantor’s revolutionary proof showed that the real numbers between 0 and 1 are uncountably infinite, and thus there are different “sizes” of infinity. This challenged the conventional understanding of mathematics and paved the way for modern set theory.

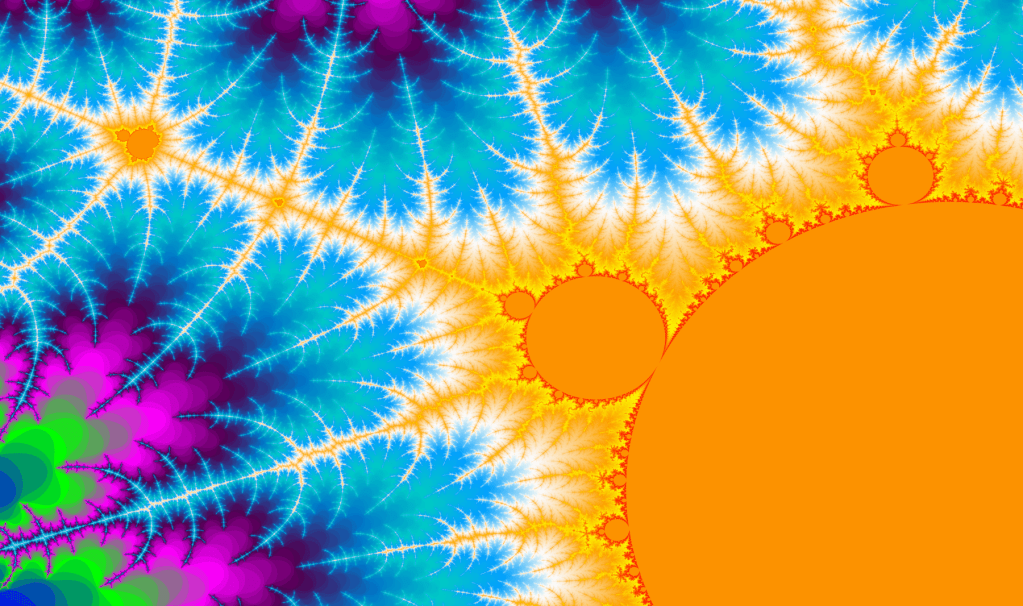
Fractals: Fractals, such as the Mandelbrot set, exhibit self-similarity—no matter how deeply you zoom in, the pattern repeats infinitely. This is a visual manifestation of infinite complexity and recursion, revealing how infinity can exist even within finite boundaries.

Infinity in Real Life

Infinity isn’t confined to abstract mathematics—it also makes appearances in the physical world:

Space and the Universe: The vastness of space is often thought of as infinite. While the observable universe is finite, the entirety of the universe is unknown and could very well be infinite, with no boundaries or edges. The idea of an ever-expanding universe also evokes infinity, as the cosmos continues to grow without limits.

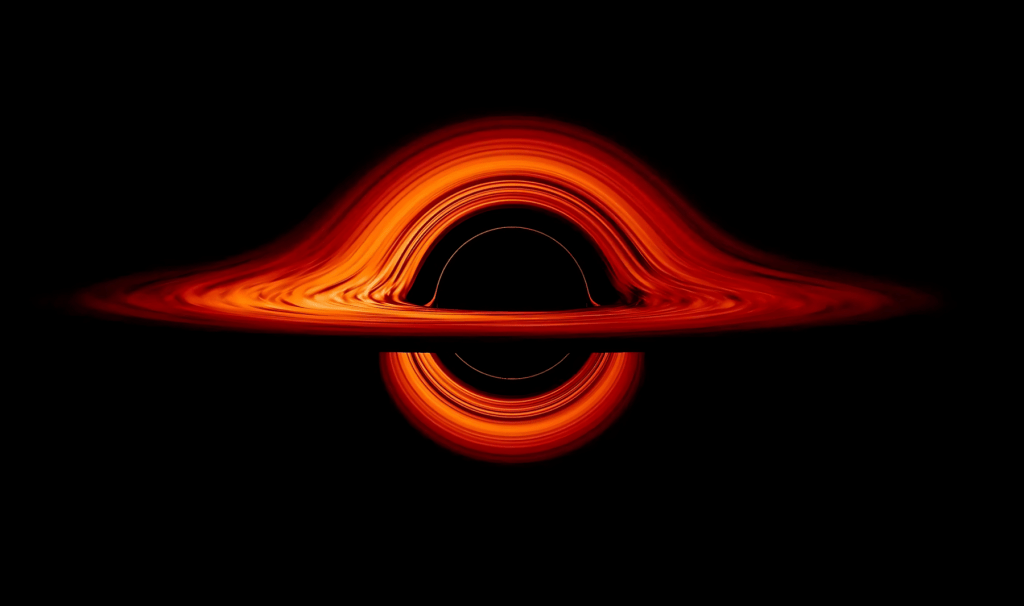
Black Holes and Singularities: In physics, black holes contain points called singularities, where the density of matter is thought to become infinite. At the singularity, the gravitational pull is so intense that not even light can escape, and current physical laws break down. One could argue that singularities are among the most enigmatic manifestations of infinity in the universe.

Infinity and Spirituality: In Indian philosophy, the concept of infinity holds profound significance, particularly in ancient texts like the Vedas and Upanishads. There is a famous mantra from the Brihadaranyaka Upanishad, and it reflects the deep philosophical notion of completeness and infinity in Indian spiritual thought. 

ॐ पूर्णमदः पूर्णमिदं पूर्णात् पूर्णमुदच्यते ।
पूर्णस्य पूर्णमादाय पूर्णमेवावशिष्यते ॥

― Verse 5.1.1, Brihadaranyaka Upanishad

Translation: “That (Brahman) is complete (infinite), this (universe) is complete (infinite); from the complete (infinite), the complete (infinite) arises. When the complete (infinite) is taken from the complete (infinite), the complete (infinite) still remains.”

This verse illustrates the paradoxical and boundless nature of infinity, where even when something is subtracted, infinity remains undiminished.

---

In summary, infinity transcends mathematics, touching on physics, philosophy, and spirituality. Its presence can even be felt in art and music. This infinity paradox challenges our understanding, appearing in everything from fractals to the cosmos. Though elusive, infinity continues to push the limits of human understanding and knowledge. Thus profoundly changing our understanding of our universe and our reality.